Prefix Algorithm

Prefix Sum Algorithm이란?

• Prefix sum (누적 합)
  • 앞부분 합을 미리 계산해 두어 이후의 구간 합 / 구간 업데이트를 아주 빠르게 처리하기 위한 기법
• 어떻게 생각을 하게 되었는가?
  • “배열의 구간 합 (sum of A[l … r])”을 반복해서 묻거나, “구간에 같은 값을 더하기”같은 연산을 반복함. 매번 구간을 더하거나 업데이트하면 O(length_of_interval)이 드는데, 이걸 O(1)(or 빠른 시간)으로 만들기 위해
• Idea : 어떤 인덱스 $i$에 해새 $prefix[i] = A[0] + A[1] + … + A[i]$를 미리 계산해 두면, 임의 구간 $A[l … r]의 합은 $prefix[r] - prefix[l - 1]$로 O(1)에 구할 수 있음

차원(Dimension)별 Prefix Sum Algorithm

1 Dimension

• 정의
  • 배열 $A[0 … n -1]$에 대해 $S[i] = \sum_{k\ =\ 0\ …\ i}\ A[k]$
• 구간 합
  • $\sum_{i = l … r}A(i) = S[r] - P[l - 1]$
    • $S[r] = A[0] + … + A[l - 1] + A[l] + … + A[r]$
    • $S[l-1] = A[0] + … + A[l-1]$
• 복잡도
  • S 계산 : O(n)
  • 구간 합 당 : O(1)

    2 Dimension

• 정의
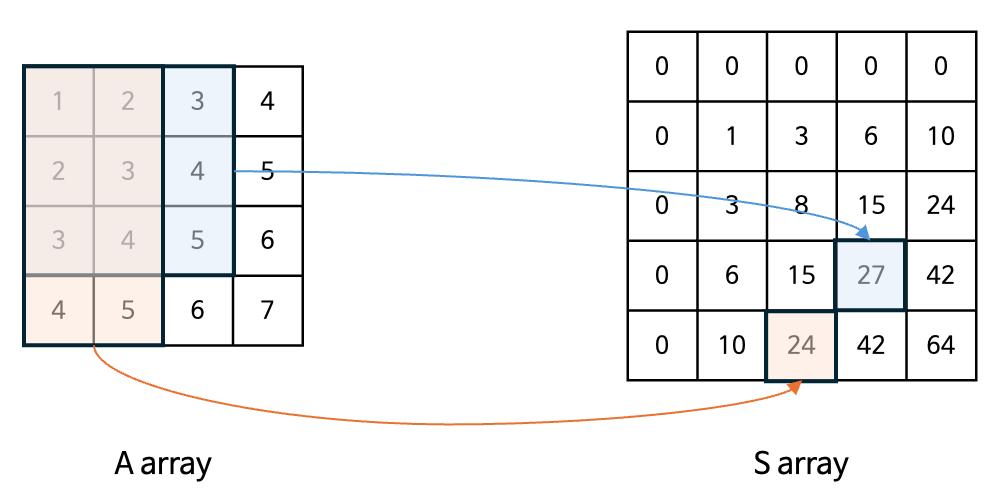
  • 배열 $A[0 … n - 1][0 … n - 1]$에 대해 $S[i][j] = \sum_{i = 0 .. n, j = 0 … n}A[i][j]$
• 구간 합
  • $S[i][j] = \sum_{x = 0 … i, y = 0 … j}A[x][y] = A[i-1][j-1] + S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1]$

응용

차분 배열 (Difference array) - 구간 업데이트

• 문제
  • “구간 $[l, r]$에 $+ v$를 반복적으로 적용” → 직접 더하면 느림
• 해결
  • $D[0 … n]$을 두고, 구간 $[l, r]$에 $+v$를 다음처럼 표시
    • $D[l] += v$
    • $D[r+1] -= v$($r+1$가 범위 밖이면 생략)
  • 그런 다음 $A[i] = prefix_of_D[i]$ (즉, $A[i] = \sum_{k = 0 … i}D[k]$)
• 동작
  • $D[l]$에서 $+v$가 시작되고 $D[r + 1]$에서 멈추므로, $l <= i <= r$인 인덱스에서만 누적합이 $v$만큼 더해짐.

2차원에 적용

[!coution]- 2차원에서는 x축, y축 두 방향으로 누적이 된다.

S[i][j] = 
	diff[i][j]
	+ 위에서 오는 누적(S[i-1][j])
	+ 왼쪽에서 오는 누적(S[i][j-1])
	- 대각선 중복(S[i-1][j-1])

• $A$를 $(n + 1) \times (m + 1)$ 쿼리 ($r_1, c_1, r_2, c_2$)에 대해

    A[r1][c1] += v
    A[r1][c2+1] -= v
    A[r2+1][c1] -= v
    A[r2+1][c2+1] += v
  

  $S[i][j] = A[i][j] + S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1]$

• 원리 (포함-배제)
  • (r1,c1) 에 +v 함으로써 (r1,c1)부터 오른쪽 아래 전체에 효과가 생김
  • (r1,c2+1) 에 -v 를 둬서 열 기준으로 오른쪽에서 효과를 제거
  • (r2+1,c1) 에 -v 를 둬서 행 기준으로 아래쪽에서 효과를 제거
  • (r2+1,c2+1) 에 +v 를 둬서 위의 두 번 제거된 교차 구간을 다시 보정 이 네 표시는 포함·배제의 2D 버전입니다.