[Python] Bagging
[Python] Bagging
Bagging
Create. Seung-Ho Ryu (Comment. Jung-In Seo)
Reference
- 파이썬 머신러닝 완벽 가이드 (Chapter. 4-3)< 실습 데이터셋 >
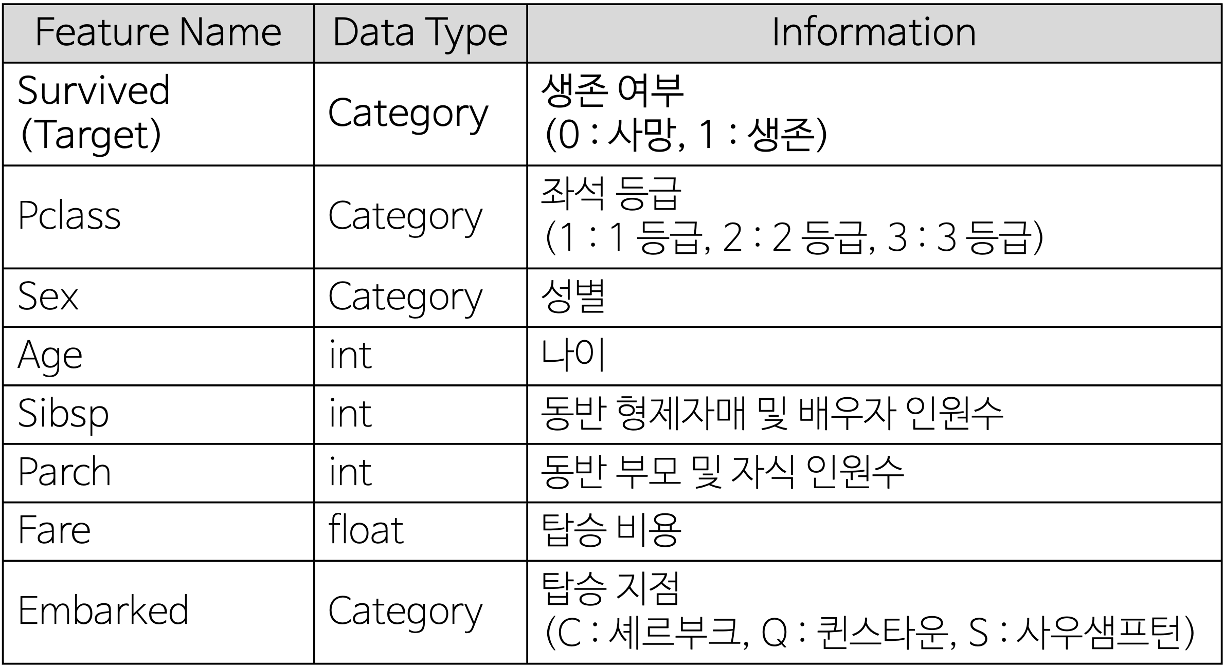
- Titanic 데이터 셋 : 타이타닉 사건(1912년도) 때 타이타닉 호에 탑승했던 승객들의 정보, 생존 여부등으로 총 11개의 Feature로 이루어져 있습니다.
- 11개의 변수 중 분석에 사용할 변수는 아래의 표에서 소개를 합니다.
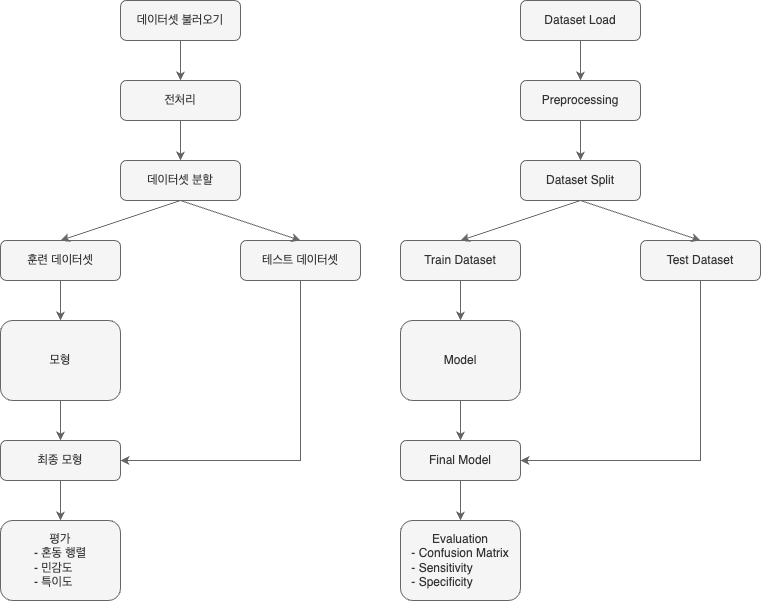
- Flow Chart
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Data Preprocessing
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split, cross_val_score, StratifiedKFold
from sklearn.preprocessing import StandardScaler, LabelEncoder
# Visualization
import seaborn as sns
import matplotlib.pyplot as plt
# warning ignore
import warnings
warnings.filterwarnings(action = 'ignore')
# Model Definition
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
# Evaluation
from sklearn.metrics import roc_curve, accuracy_score, confusion_matrix, roc_auc_score
1. 데이터 불러오기
1
2
3
4
# 데이터 불러오기
titanic = pd.read_csv('./Data/Titanic.csv')
titanic
| Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th… | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 886 | 0 | 2 | Montvila, Rev. Juozas | male | 27.0 | 0 | 0 | 211536 | 13.0000 | NaN | S |
| 887 | 1 | 1 | Graham, Miss. Margaret Edith | female | 19.0 | 0 | 0 | 112053 | 30.0000 | B42 | S |
| 888 | 0 | 3 | Johnston, Miss. Catherine Helen “Carrie” | female | NaN | 1 | 2 | W./C. 6607 | 23.4500 | NaN | S |
| 889 | 1 | 1 | Behr, Mr. Karl Howell | male | 26.0 | 0 | 0 | 111369 | 30.0000 | C148 | C |
| 890 | 0 | 3 | Dooley, Mr. Patrick | male | 32.0 | 0 | 0 | 370376 | 7.7500 | NaN | Q |
891 rows × 11 columns
2. 전처리
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 가족 변수 추가
titanic['FamSize'] = titanic['SibSp'] + titanic['Parch'] # FamSize = 형제 및 배우자 수 + 부모님 및 자녀 수
# 분석에 사용할 변수만 선택
Use_Columns = ['Survived', 'Pclass', 'Sex', 'Age', 'FamSize', 'Fare', 'Embarked']
titanic = titanic[Use_Columns]
# 결측값 제거
titanic.dropna(subset = ['Age'], axis = 0, inplace = True)
# 변수 형태 변경
titanic[['Survived', 'Pclass', 'Sex', 'Embarked']] = titanic[['Survived', 'Pclass', 'Sex', 'Embarked']].astype('category')
titanic['Age'] = titanic['Age'].astype('int')
# One-Hot-Encoding
titanic = pd.get_dummies(titanic, columns = ['Pclass', 'Sex', 'Embarked'], drop_first = True)
3. 데이터 탐색
1
2
# 변수 형태
titanic.info()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
<class 'pandas.core.frame.DataFrame'>
Index: 714 entries, 0 to 890
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Survived 714 non-null category
1 Age 714 non-null int64
2 FamSize 714 non-null int64
3 Fare 714 non-null float64
4 Pclass_2 714 non-null bool
5 Pclass_3 714 non-null bool
6 Sex_male 714 non-null bool
7 Embarked_Q 714 non-null bool
8 Embarked_S 714 non-null bool
dtypes: bool(5), category(1), float64(1), int64(2)
memory usage: 26.6 KB
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
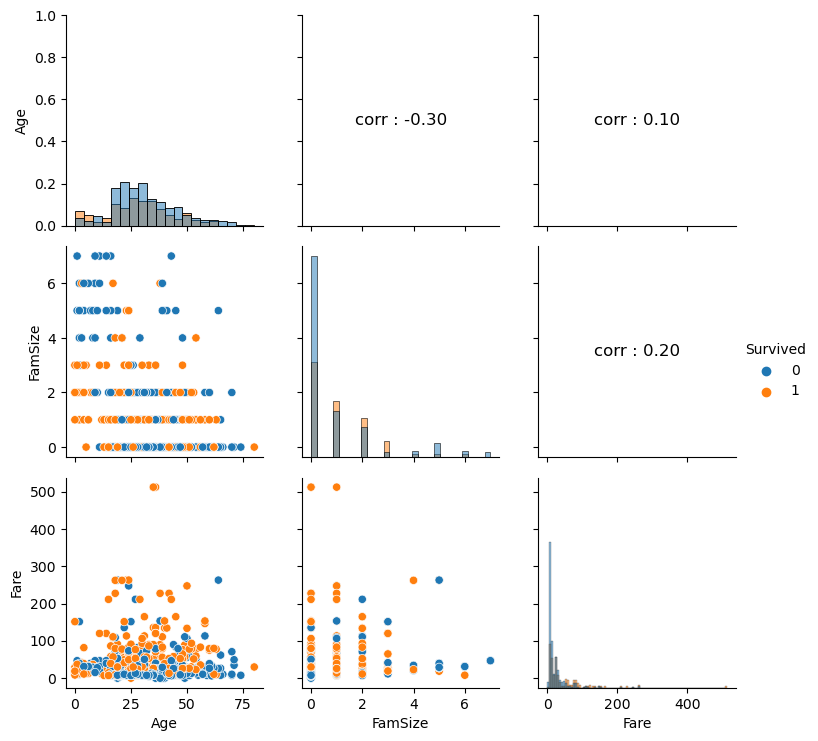
# 수치형 변수 시각화
def numberic_plot(df, target):
g = sns.PairGrid(df, hue = target) # 주어진 데이터 컬럼에 대한 모든 조합을 만들어주는 빈 틀을 위한 코드
g.map_diag(sns.histplot) # 삼각행렬의 중간 부분
g.map_lower(sns.scatterplot) # 아래 부분
# 상관 계수 행렬을 구하고 상관 계수 값 표시
corr_matrix = df.corr()
for i, j in zip(*plt.np.triu_indices_from(g.axes, k = 1)): # np.triu_indices_from : 삼각행렬의 위쪽 삼각형의 인덱스 (k = 0 : 대각 행렬 포함, 1 : 제외)
g.axes[i, j].annotate(f"corr : {corr_matrix.iloc[i, j]:.2f}", # 상관계수
(0.5, 0.5), xycoords = "axes fraction", ha = 'center', va = 'center', # 중앙 정렬
fontsize = 12, # 글자 크기
color = 'black') # 글자 색
g.add_legend() # 범례 표시
plt.show()
Columns = ['Age', 'FamSize', 'Fare', 'Survived'] # 수치형 변수
numberic_plot(titanic[Columns], 'Survived')
4. 데이터 분할
1
2
3
4
5
6
7
8
# 생존 여부 변수를 Target으로 지정
y = titanic['Survived']
# 나머지 변수들을 예측 변수로 지정
X = titanic.drop(['Survived'], axis = 1)
# 75 : 25로 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
5. 배깅(Bagging)
from sklearn.ensemble import BaggingClassifier
# 배깅(Bagging) 모형 정의(파라미터 기본값)
BaggingClassifier(
estimator = None, # 배깅에 사용할 기본 분류기
n_estimators = 10, # 배깅에서 사용할 기본 분류기의 개수
max_samples = 1.0, # 각 분류기를 학습할 때 사용할 학습 데이터의 샘플 크기를 지정
bootstrap = True, # 데이터 샘플 복원 추출 여부
max_features = 1.0, # 각 분류기가 학습할 때 사용할 특성의 수
bootstrap_features = False, # 특성 복원 추출 여부
oob_score = True, # oob 점수 계산 여부
n_jobs = None, # 사용할 CPU 개수
random_state = None # 고정값
)
5-1. 모형 정의
1
2
3
4
5
6
7
8
9
10
11
12
13
# 배깅에 사용할 기본 모형 정의
DT = DecisionTreeClassifier(
max_depth = None, # 트리의 최대 깊이
min_samples_split = 2, # 노드 분할에 필요한 최소 샘플 수
min_samples_leaf = 1, # 말단(Leaf) 노드에 필요한 최소 샘플 수
max_features = None, # 각 분할을 위해 검사할 특징의 수
random_state = 0 # 고정값
)
# 배깅 모형 정의
Bagging = BaggingClassifier(estimator = DT, # 기본 분류기
n_jobs = -1, # 사용할 CPU 개수
random_state = 0) # 고정값
5-2. 모형 훈련
1
Bagging.fit(X_train, y_train)
BaggingClassifier(estimator=DecisionTreeClassifier(random_state=0), n_jobs=-1,random_state=0)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
BaggingClassifier(estimator=DecisionTreeClassifier(random_state=0), n_jobs=-1,random_state=0)
DecisionTreeClassifier(random_state=0)
DecisionTreeClassifier(random_state=0)
5-3. 모형 평가
1
2
Bagging_pred = Bagging.predict(X_test)
Bagging_pred
1
2
3
4
5
6
7
8
9
array([1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1,
1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1,
1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0,
1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0,
0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0,
1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0,
1, 0, 1])
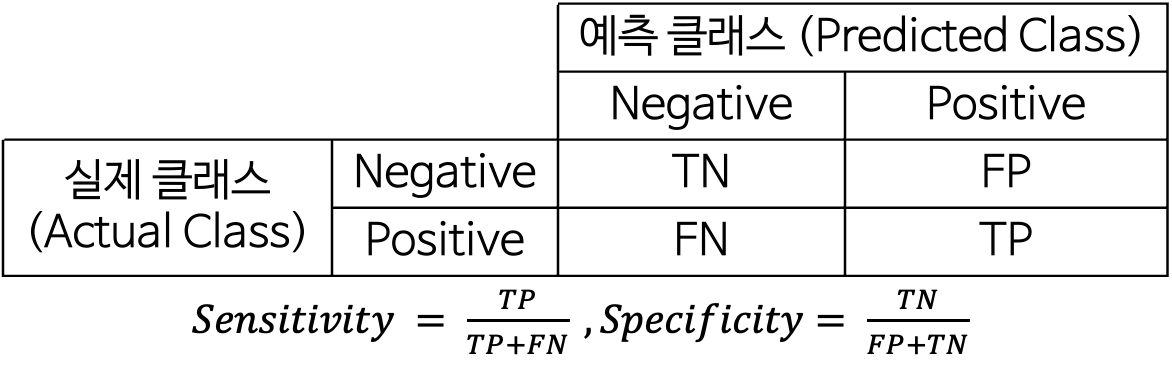
5-3-1. Confusion Matrix
1
2
3
4
5
6
7
8
Bagging_cfx = confusion_matrix(y_test, Bagging_pred) # Confusion Matrix
Bagging_sensitivity = Bagging_cfx[1, 1] / (Bagging_cfx[1, 0] + Bagging_cfx[1, 1]) # 민감도 계산
Bagging_specificity = Bagging_cfx[0, 0] / (Bagging_cfx[0, 0] + Bagging_cfx[0, 1]) # 특이도 계산
print(f"Bagging 정확도(accuracy) : {accuracy_score(y_test, Bagging_pred) * 100 :.2f}%")
print(f"Bagging Confusion_Matrix :\n{Bagging_cfx}")
print(f"Bagging 민감도(sensitivity) : {Bagging_sensitivity * 100 :.2f}%")
print(f"Bagging 특이도(specificity) : {Bagging_specificity * 100 :.2f}%")
1
2
3
4
5
6
Bagging 정확도(accuracy) : 78.21%
Bagging Confusion_Matrix :
[[83 20]
[19 57]]
Bagging 민감도(sensitivity) : 75.00%
Bagging 특이도(specificity) : 80.58%
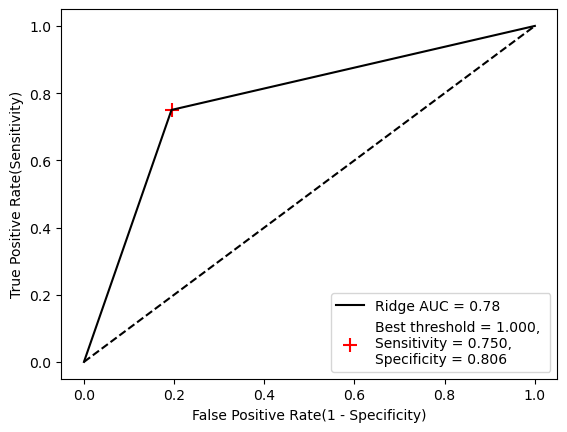
5-3-2. ROC 곡선
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Bagging_pred = Bagging.predict(X_test)
fpr, tpr, thresholds = roc_curve(y_test, Bagging_pred)
J = tpr - fpr
ix = np.argmax(J) # 가장 큰 원소의 위치(최대값의 인덱스)
best_thresh = thresholds[ix]
#plot roc and best threshold
sens, spec = tpr[ix], 1 - fpr[ix]
# plot the roc curve for the model
plt.plot([0,1], [0,1], linestyle = '--', markersize = 0.01, color = 'black') # 중간 기준 선
plt.plot(fpr, tpr, marker = '.', color = 'black', markersize = 0.01, label = "Ridge AUC = %.2f" % roc_auc_score(y_test, Bagging_pred))
plt.scatter(fpr[ix], tpr[ix], marker = '+', s = 100, color = 'r',
label = f"Best threshold = {best_thresh:.3f}, \nSensitivity = {sens:.3f}, \nSpecificity = {spec:.3f}")
# axis labels
plt.xlabel("False Positive Rate(1 - Specificity)")
plt.ylabel("True Positive Rate(Sensitivity)")
plt.legend(loc = 4)
# show the plot
plt.show()
This post is licensed under CC BY 4.0 by the author.